MCQ Questions for Class 10 Science Chemical Reactions and Equations with Answers: Students CBSE Board Exams 2020 Time Table is out now. The board is going to conduct a Class 10 CBSE Science Exam on 4th March 2020. As per their official notification, this time CBSE Exam Pattern 2020 is having slight changes. The board decided to add MCQ Questions for Class 10 CBSE Board Exams. Here, you will find important MCQs from CBSE Class 10 Science Chapter 1 Chemical Reactions and Equations along with the answers.
CBSE Class 10 Science MCQs of Chemical Reactions and Equations with Answers
Such Multiple Choice Type Questions are ideal to brushes your basic concepts to answer in CBSE Class 10 Science Exam 2020. Also, this objective type questions will help you to adjust with all various approaches. In this article, we have provided Chemical Reactions and Equations MCQ Questions for Class 10 CBSE Science Exam 2020 with a detailed explanation of answers. It makes easy to grasp the in-depth concept and logic of the question. So, practice below provided MCQ’s of CBSE Class 10 Chapter 1 Chemical Reactions and Equations topics to score maximum marks in your pre-board and final board exams.
Question 1. Which of the following is a displacement reaction?

Answer/ Explanation
Answer: b
Explaination: Reason: Here sodium (Na) displaces to form sodium hydroxide.
Question 2. Magnesium ribbon is rubbed before burning because it has a coating of
(a) basic magnesium carbonate
(b) basic magnesium oxide
(c) basic magnesium sulphide
(d) basic magnesium chloride
Answer
Answer: a
Question 3. Which of the following statements about the given reaction are correct?
3Fe (s) + 4H2O (g) → Fe3O4 (s) + 4 H2 (g)
(i) Iron metal is getting oxidised
(ii) Water is getting reduced
(iii) Water is acting as reducing agent
(iv) Water is acting as oxidising agent
(a) (i), (zi) and (iii)
(b) (in) and (iv)
(c) (i), (ii) and (iv)
(d) (ii) and (iv)
Answer
Answer: c
Question 4. Which of the following are exothermic processes?
(i) Reaction of water with quick lime
(ii) Dilution of an acid
(iii) Evaporation of water
(iv) Sublimation of camphor (crystals)
(a) (i) and (ii)
(b) (ii) and (iii)
(c) (i) and (iv)
(d) (ii) and (iv)
Answer/ Explanation
Answer: a
Explaination: Reason: In both the cases, heat energy is evolved.
Question 5. Oxidation is a process which involves
(a) addition of oxygen
(b) addition of hydrogen
(c) removal of oxygen
(d) removal of hydrogen
Answer
Answer: a
Question 6. The process of reduction involves
(a) addition of oxygen
(b) addition of hydrogen
(c) removal of oxygen
(d) removal of hydrogen
Answer
Answer: b
Question 7. Three beakers labelled as A, B and C each containing 25 ml of water were taken. A small amount of NaOH, anhydrous CuSO4 and NaCl were added to the beakers A, B and C respectively. It was observed that there was an increase in the temperature of the solution contained in beakers A and B, whereas in case of beaker C, the temperature of the solution falls. Which one of the following statement(s) is (are) correct?
(i) In beakers A and B, exothermic process has occurred.
(ii) In beakers A and B, endothermic process has occuBftd.
(iii) In beaker C exothermic process has occurred.
(iv) In beaker C endothermic process has occurred.
(a) (i) only
(b) (ii) only
(c) (i) and (iv)
(d) (iv), (ii) and (iii)
Answer
Answer: c
Question 8. Give the ratio in which hydrogen and oxygen are present in water by volume.
(a) 1:2
(b) 1:1
(c) 2:1
(d) 1:8
Answer
Answer: a
Question 9. Which among the following statement(s) is (are) true?
Exposure of silver chloride to sunlight for a long duration turns grey due to
(i) the formation of silver by decomposition of silver chloride
(ii) sublimation of silver chloride
(iii decomposition of chlorine gas from silver chloride
(iv) oxidation of silver chloride
(a) (i) only
(b) (i) and (iii)
(c) (ii) and (iii)
(d) (iv) only
Answer
Answer: a
Question 10. MnO2 + 4HCl → 2 + 2H2O + Cl2
Identify the substance oxidized in the above . equation.
(a) MnCl2
(b) HCl
(c) H2O
(d) MnO2
Answer/ Explanation
Answer: d
Explaination: Reason: In this reaction HCl is oxidised to Cl2, whereas MnO2 is reduced to MnCl2.
Question 11. A substance ‘X’ is used in white-washing and is obtained by heating limestone in the absence of air. Identify ‘X’.
(a) CaOCl2
(b) Ca (OH)2
(c) CaO
(d) CaCO3
Answer/ Explanation
Answer:
Explaination:
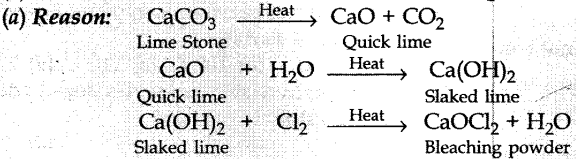
Question 12. When Ag is exposed to air it gets a black coating of
(a) AgNO3
(b) Ag2S
(c) Ag2O
(d) Ag2CO3
Answer
Answer: b
Question 13. Which of the following is an endothermic process?
(a) Dilution of sulphuric acid
(b) Sublimation of dry ice
(c) Condensation of water vapours
(d) Respiration in human beings
Answer
Answer: b
Question 14. In the double displacement reaction between aqueous potassium iodide and aqueous lead nitrate, a yellow precipitate of lead iodide is formed. While performing the activity if lead nitrate is not available, which of the following can be used in place of lead nitrate?
(a) Lead sulphate (insoluble)
(&) Lead acetate
(c) Ammonium nitrate
(d) Potassium sulphate
Answer
Answer: b
Question 15. What type of chemical reactions take place when electricity is passed through water?
(a) Displacement
(b) Combination
(c) Decomposition
(d) Double displacement
Answer/ Explanation
Answer: c
Explaination:

Question 16. Select the oxidising agent for the following reaction:
H2S + I2 > 2HI + S
(a) I2
(b) H2S
(C) HI
(d) S
Answer
Answer: a
Question 17. A substance added to food containing fats and oils is called:
(a) Oxidant
(b) Rancid
(c) Coolant
(d) Antioxidant
Answer
Answer: d
Question 18. The condition produced by aerial oxidation of fats and oils in foods marked by unpleasant smell and taste is called:
(a) antioxidation
(b) reduction
(c) rancidity
(d) corrosion
Answer
Answer: c
Question 19. Electrolysis of water is a decomposition reaction. The mole ratio of hydrogen and oxygen gases liberated during electrolysis of water is:
(a) 1 : 1
(b) 2:1
(c) 4:1
(d) 1:2
Answer
Answer: b
Question 20. When S02 gas is passed through saturated solution of H2S, which of the following reaction occurs?
(a) SO2 + 2H2S → 2H20 + 3S
(b) SO2 + 2H2S → H20 + 3S
(c)SO2 + H2S → H2O + S
(d) SO2 + H2O → SO3 + H2
Answer
Answer: a
Question 21. Name the products formed when iron filings are heated with dilute hydrochloric acid
(a) Fe (III) chloride and water
(b) Fe (II) chloride and water
(c) Fe (II) chloride and hydrogen gas
(d) Fe (III) chloride and hydrogen gas
Answer/ Explanation
Answer: d
Explaination: Reason: 2Fe + 6HCl → 2FeCl3 (Iron (III) chloride) + 3H2
Question 22. Pb + CuCl2 → PbCl2 + Cu
The above reaction is an example of:
(a) combination
(b) double displacement
(c) decomposition
(d) displacement
Answer
Answer: d
Question 23. Which of the following gases can be used for storage (a) Carbon dioxide or Oxygen
(b) Nitrogen or Oxygen
(c) Carbon dioxide or Helium
(d) Helium or Nitrogen
Answer
Answer: d
Question 24. A dilute ferrous sulphate solution was gradu¬ally added to the beaker containing acidified permanganate solution. The light purple colour of the solution fades and finally disap¬pears. Which of the following is the correct explanation for the observation?
(a) KMnO4 is an oxidising agent, it oxidises FeSO4.
(b) FeSO4 acts as an oxidising agent and oxidises KMNO4.
(c) The colour disappears due to dilution; no reaction is involved.
(d) KMnO4 is an unstable compound and de-composes in presence of FeSO4. to a colourless compound.
Answer
Answer: a
Question 25. In which of the following chemical equations, the abbreviations represent the correct states of the reactants and products involved at reaction temperature?
(a) 2H2 (l) + O2 (l) > 2H2O(g)
(b) 2H2 (g) + O2 (l) > 2H2O (l)
(c) 2H2 (g) + O2 (g) > 2H2O (l)
(d) 2H2 (g) +O2 (g) > 2H2O (g)
Answer
Answer: d
Question 26. When green coloured ferrous sulphate crystals are heated, the colour of the crystal changes because
(a) it is decomposed to ferric oxide
(b) it loses water of crystallisation
(c) it forms SO2
(d) it forms SO3
Answer
Answer: b
Fill in the Blanks
1. The addition of oxygen to a substance is called …………. whereas removal of oxygen is called …………. .
2. The addition of hydrogen to a substance is called …………. whereas removal of hydrogen is called …………. .
3. Precipitation reactions produce insoluble …………. .
4. Reactions in which energy is given out are known as …………. .
5. Reaction in which an element displaces another element from its compound is called …………. .
6. Two antioxidants which are usually added to fat and oil containing foods to prevent rancidity, are …………., …………. .
7 …………. is the process in which metals are eaten up gradually by the action of air, moisture or a chemical on
their surface.
8. 2 FeSO4 → Fe2O3 + SO2 + ………….
9. Na2SO4 + BaCl2 → …………. + 2NaCl
10. Complete the missing components/variables given as x and y in the following reactions:
(a) Pb (NO3)2 (aq) + 2KI (aq) → Pbl2 (x) + 2KNO3 (y)
(b) Cu (s) + 2AgNO3 (aq) → Cu (NO3)2 (aq) + x (s)
Answers
1. oxidation, reduction
2. reduction, oxidation
3. salts
4. exothermic reactions
5. displacement reaction
6. BHA and BHT
7. Corrosion
8. SO3
9. BaSO4
10. (a) x → (s); y → (aq);
(b) x → 2Ag
you can also practice more MCQ Questions for Class 10 Science Chemical Reactions and Equations with Answers from here.
We hope the given MCQ Questions for Class 10 Science Chemical Reactions and Equations with Answers will help you. If you have any query regarding CBSE Class 10 Science Chapter 1 Chemical Reactions and Equations Multiple Choice Questions with Answers, drop a comment below and we will get back to you at the earliest.
